[백준] 1328번: 고층 빌딩

📌 문제

https://www.acmicpc.net/problem/1328

📌 설명

접근 방법만 잘 찾으면 어렵지 않은 문제라고 생각한다. 개인적으로 bottom-up 접근법보다 top-down 접근법으로 생각하는 것이 도움이 되었다. 물론 후술할 풀이는 bottom-up으로 접근하던 top-down으로 접근하던 충분히 떠올릴 수 있는 풀이이다. 단, 높이가 N인 빌딩보다 1인 빌딩을 움직이는 것이 도움이 될 것이다.

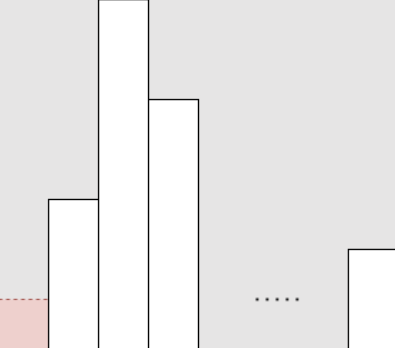
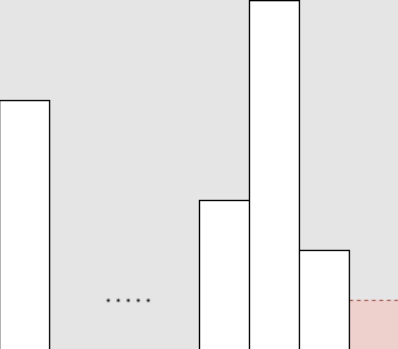
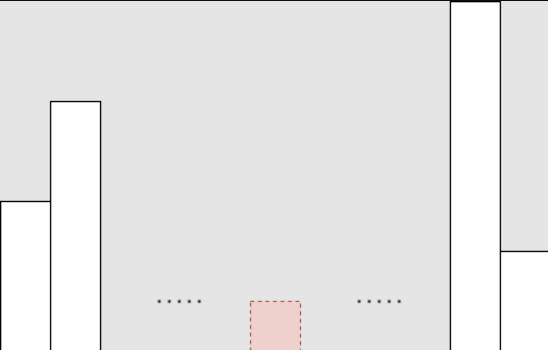
N개의 빌딩이 랜덤하게 배치되었다고 가정하자. 왼쪽에서 봤을 때 빌딩의 수를 L, 오른쪽에서 봤을 때 빌딩의 수를 R이라고 하자. 이제 높이가 1인 빌딩을 제외하자. N은 N - 1이 될 것이며, L, R은 높이가 1인 빌딩에 기존에 어디에 있었는지에 따라 달라진다.

높이가 1인 빌딩이 가장 왼쪽에 위치했다면 L은 L - 1, R은 그대로 유지된다.

 높이가 1인 빌딩이 가장 오른쪽에 위치했다면 L은 그대로 유지되고 R은 R - 1이 된다.

 높이가 1인 빌딩이 중간에 위치했다면 L, R 모두 그대로 유지된다. 중간에 위치하는 경우는 총 n - 2번 존재한다.

점화식으로 표현해보자. dp[n][l][r]을 빌딩의 수가 n, 왼쪽에서 본 빌딩의 수가 l, 오른쪽에서 본 빌딩의 수가 r일 때 가능한 빌딩 배치의 수라고 하자. 점화식은 다음과 같다.

dp[n][l][r] = dp[n - 1][l - 1][r] + dp[n - 1][l][r - 1] + dp[n - 1][l][r] * (n - 2)

📌 코드

#include <iostream>

#define MOD 1000000007

using namespace std;

typedef long long ll;

ll dp[101][101][101];

int main() {
	int n, l, r;
	cin >> n >> l >> r;

	dp[1][1][1] = 1;

	for (int i = 2; i <= n; i++) {
		dp[i][1][i] = 1; // i, i - 1, ..., 2, 1으로 순차적 배치
		dp[i][i][1] = 1; // 1, 2, ..., i - 1, i으로 순차적 배치
	}

	for (int i = 2; i <= n; i++) {
		for (int j = 1; j <= l; j++) {
			for (int k = 1; k <= r; k++) {
				dp[i][j][k] = dp[i - 1][j - 1][k] + dp[i - 1][j][k - 1] + dp[i - 1][j][k] * (i - 2);
				dp[i][j][k] %= MOD;
			}
		}
	}

	cout << dp[n][l][r];
}