[백준] 1621번: 조삼모사

📌 문제

https://www.acmicpc.net/problem/1621

📌 설명

 원숭이가 N개의 바나나를 가져간다. 두 가지 선택지가 있는데, 바나나 하나만 가져가거나 K개를 한꺼번에 가져가는 방법이 있다. 하나만 가져가는 경우 바나의 무게만큼 시간이 걸리며 K개를 한꺼번에 가져가면 C의 시간이 걸린다. 원숭이가 바나나를 모두 옮기는 데 걸리는 최소 시간과 한꺼번에 옮기는 행위의 횟수, K개 묶음의 왼쪽 위치를 오름차순으로 출력해야 한다. 답이 여러 개인 경우 한꺼번에 옮기는 행위가 최소가 되는 상황을 선택해야 한다.

 N개의 바나나를 옮기는 데 최소 시간을 구해야 하므로 DP를 사용한다. 또한 K개 묶음의 왼쪽 위치를 출력해야 하므로 이를 역추적하는 배열(route) 또한 추가로 필요하다.

 dp 배열은 현재 바나나를 낱개로 들고 가는 것이 이득인지, 묶어서 가져가는 것이 이득인지 구분하여 초기화한다. route 배열 또한 적절하게 초기화해야 한다. 참고로 dp 배열은 현재 바나나를 들고 갔을 때 최소 시간이다.

📌 코드

#include <iostream>
#include <algorithm>
#include <stack>

using namespace std;

int weight[1000001]; // 바나나의 무게
int dp[1000001];
int route[1000001]; // 경로 역추적
// route[i]: i보다 작거나 같은 바나나 중 가장 가까운 바나나 묶음의 첫 번째 바나나 인덱스

int main() {
	int n, k, c; // 바나나의 수, 한 번에 들고갈 수 있는 수, 걸리는 시간
	cin >> n >> k >> c;

	for (int i = 1; i <= n; i++) {
		cin >> weight[i];
	}

	for (int i = 1; i <= n; i++) {
		if (i < k) {
			dp[i] = dp[i - 1] + weight[i];
		}
		else {
			int case1 = dp[i - k] + c; // 현재 바나나를 묶는다면
			int case2 = weight[i] + dp[i - 1]; // 현재 바나나 하나만 들고 간다면

			if (case1 < case2) {
				dp[i] = case1;
				route[i] = i - k + 1;
			}
			else {
				dp[i] = case2;
				route[i] = route[i - 1];
			}
		}
	}

	cout << dp[n] << "\n";

	stack<int> s;
	int idx = n;
	int cnt = 0;
	while (route[idx] > 0) {
		cnt++;
		s.push(route[idx]);
		idx = route[idx] - 1;
	}

	cout << cnt << "\n";

	while (!s.empty()) {
		cout << s.top() << " ";
		s.pop();
	}
}

---

	for (int i = 1; i <= n; i++) {
		if (i < k) {
			dp[i] = dp[i - 1] + weight[i];
		}
		else {
			int case1 = dp[i - k] + c; // 현재 바나나를 묶는다면
			int case2 = weight[i] + dp[i - 1]; // 현재 바나나 하나만 들고 간다면

			if (case1 < case2) {
				dp[i] = case1;
				route[i] = i - k + 1;
			}
			else {
				dp[i] = case2;
				route[i] = route[i - 1];
			}
		}
	}

 i < k라면 현재 바나나를 묶음으로 가져갈 수 없다. 따라서 이전 바나나의 dp에 현재 바나나의 무게를 더한 값으로 초기화한다.

 현재 바나나를 묶음으로 들고 갈 수 있는 경우 낱개로 가져가는 것과 묶음으로 가져가는 것 중 어느 것이 이득인지 판단해야 한다. 만약 묶는 것이 이득이라면 dp를 case1으로 초기화하고 route를 묶음의 왼쪽 인덱스로 초기화한다. 그렇지 않다면 case2로 dp를 초기화하고 이전 route로 route를 초기화한다.

	cout << dp[n] << "\n";

	stack<int> s;
	int idx = n;
	int cnt = 0;
	while (route[idx] > 0) {
		cnt++;
		s.push(route[idx]);
		idx = route[idx] - 1;
	}

	cout << cnt << "\n";

	while (!s.empty()) {
		cout << s.top() << " ";
		s.pop();
	}

 route 배열은 stack으로 재정렬 후 묶음의 개수와 함께 올바르게 출력하였다.

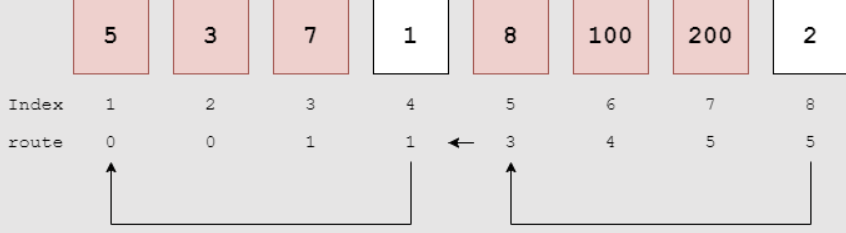
 route 배열을 역추적하는 과정을 표현한 것이다. K=3이라면 붉게 표시된 바나나를 묶음으로 가져가야 한다. route는 현재 인덱스 이전 묶음 중 가장 가까운 묶음의 왼쪽 인덱스가 들어있다.