(백준) 2015번 - 수들의 합 4

문제

https://www.acmicpc.net/problem/2015

풀이

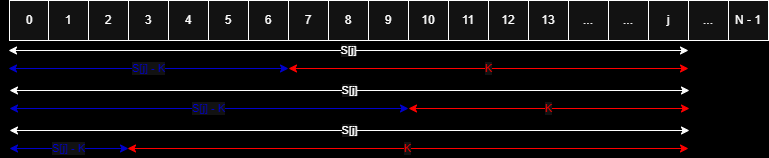
S 를 누적 합 배열이라고 하자. S[i] 는 A[0] 부터 A[i] 까지의 누적 합의 값이 저장되어 있다. 그렇다면 i부터 j까지의 부분 합은 S[j] - S[i - 1] 로 구할 수 있다.

다만, $N$의 최대값은 200,000이고, 시간 제한은 2초이므로, 이중 for문을 통해 부분 합을 구하게 되면 시간 초과가 발생한다(약 400억).

우리가 원하는 상황은 S[j] - S[i - 1] = K가 되는 상황이다. 식을 변형하면 S[i - 1] = S[j] - K가 된다. 이는 곧 현재 누적 합이 S[j]일 때, 이전의 누적 합이 S[j] - K인 경우를 찾아야 한다는 의미이다.

위 상황은 이전의 누적 합이 S[j] - K인 경우가 세 번 존재하므로, 구간 $[x, j] (0 \leq x \leq j)$ 에 존재하는 구간 합이 $K$인 경우는 세 번 존재한다.

이전의 누적 합의 등장 횟수를 해시 맵으로 관리한다. 주의해야 할 점은 S[j] - K가 0이 되는 상황이다. 이는 S[j] 자체가 $K$인 상황이며, 초기에 해시 맵에 누적 합이 0인 경우 등장 횟수가 1임을 설정해주어야 한다.

코드

#include <iostream>
#include <vector>
#include <map>

using namespace std;

int main() {
	int n, k;
	cin >> n >> k;
	vector<int> v(n);
	for (int i = 0; i < n; i++) {
		cin >> v[i];
	}

	int cumsum = 0;
	long long cnt = 0;
	map<int, int> m;
	m[0] = 1; // 자기 자신이 k인 경우

	for (int i = 0; i < n; i++) {
		cumsum += v[i];
		cnt += m[cumsum - k];
		m[cumsum]++;
	}

	cout << cnt;
}

주의해야 할 점은 cnt의 자료형이다. $N$은 최대 200,000이며, 이 때 만들어지는 부분 합의 수는 약 200억이다($N(N+1)/2$). 따라서 int대신 long long으로 선언해야 한다.

시간복잡도

for문에서 $O(N)$, map에서 $O(log(N))$이다. map은 내부적으로 레드-블랙 트리로 구현되어 있으므로, 삽입 및 조회 시의 시간복잡도가 $O(log(N))$이다.

따라서 전체 시간복잡도는 $O(Nlog(N))$이다.

공간복잡도

vector, map에서 각각 $O(N)$이므로, 전체 공간복잡도는 $O(N)$이다.