최소 스패닝 트리

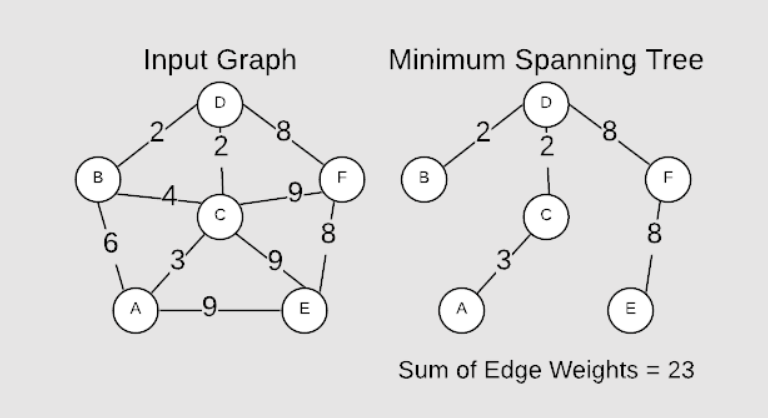
최소 스패닝 트리(Minimum Spanning Tree, MST)는 가장 적은 가중치로 그래프의 모든 정점을 연결하는 트리를 말한다.

스패닝 트리는 그래프 내의 모든 정점을 포함하면서 사이클이 없는 트리를 말한다.

특징

• 정점의 개수가 $n$개일 때, 간선의 개수는 반드시 $n-1$개이다.
• 트리이므로 사이클이 존재하지 않는다.
• 모든 정점이 연결되어야 한다.
• 간선의 가중치가 모두 다르다면 MST는 유일하게 하나 존재한다.

알고리즘

MST를 찾기 위해 사용되는 알고리즘은 프림 알고리즘, 크루스칼 알고리즘이 존재한다. 두 알고리즘 모두 그리디 성격을 띄고 있다.

프림 알고리즘

동작 과정은 다음과 같다.

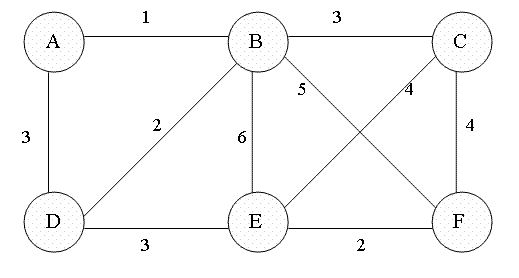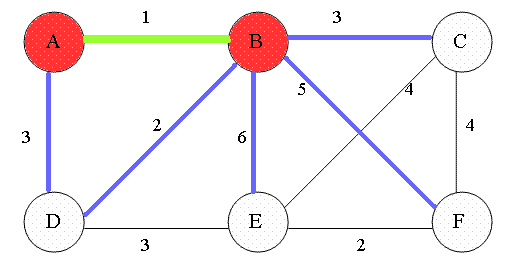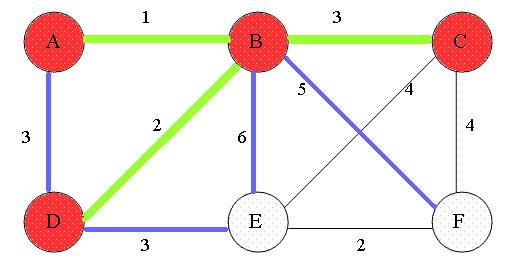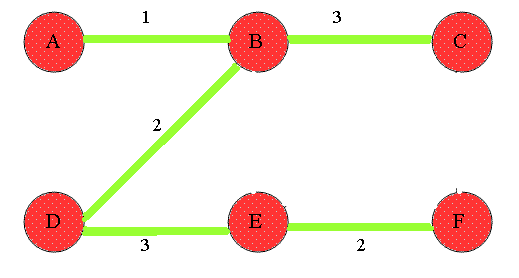
1. 임의의 정점 하나를 선택한다.
2. 현재 트리에서 연결된 정점들과 연결되지 않는 간선들 중, 가중치가 가장 작은 간선을 선택하여 트리에 추가한다.
3. 이 과정을 모든 정점들이 연결될 때까지 반복한다.

---

가중치가 가장 작은 간선을 선택하기 위해 우선순위 큐를 사용한다.

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

typedef pair<int, int> pii; // { 정점 번호, 가중치 }

// V: 정점의 개수, adj: 인접 리스트
int prim(int V, const vector<vector<pii>>& adj) {
    int total = 0; // MST의 총 가중치 합
    
    vector<int> visited(V + 1);
    
    priority_queue<pii, vector<pii>, greater<pii>> pq;

    // 시작 노드를 1번 노드라고 가정
    pq.push({0, 1});

    while (!pq.empty()) {
        int w = pq.top().first;
        int u = pq.top().second;
        pq.pop();

        // 이미 방문한 정점(이미 MST에 포함된 정점)이면 pass
        if (visited[u]) continue;

        visited[u] = 1;
        total += w;
        
        // 현재 정점과 연결된 인접 정점들을 확인하여
        for (auto& edge : adj[u]) {
            int v = edge.first;
            int cost = edge.second;

            // 방문하지 않은 정점이라면 큐에 삽입한다.
            if (!visited[v]) {
                pq.push({cost, v});
            }
        }
    }

    return total;
}

---

시간복잡도는 $O(ElogV)$이다. 최악의 경우 모든 간선에 대해 힙 연산을 수행하고, 일반적으로 $E \leq V^2$이기 때문이다.

크루스칼 알고리즘

동작 과정은 다음과 같다.

1. 모든 간선의 가중치를 오름차순으로 정렬한다.
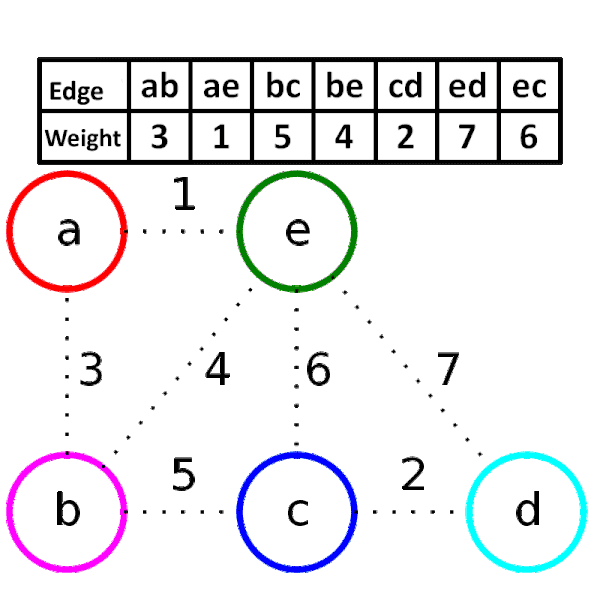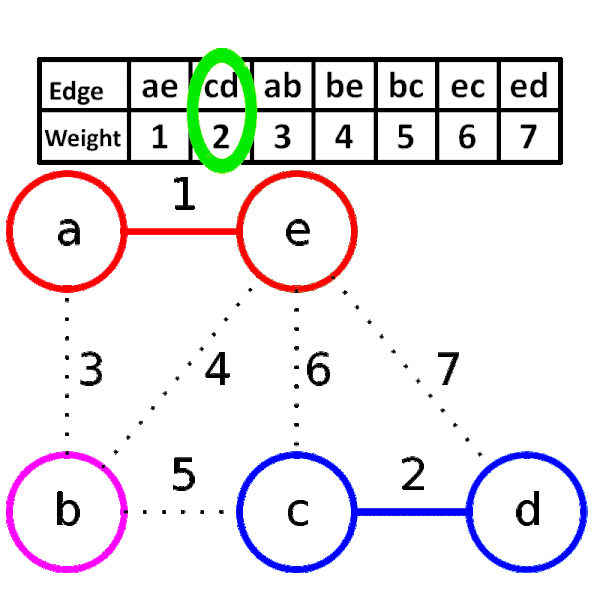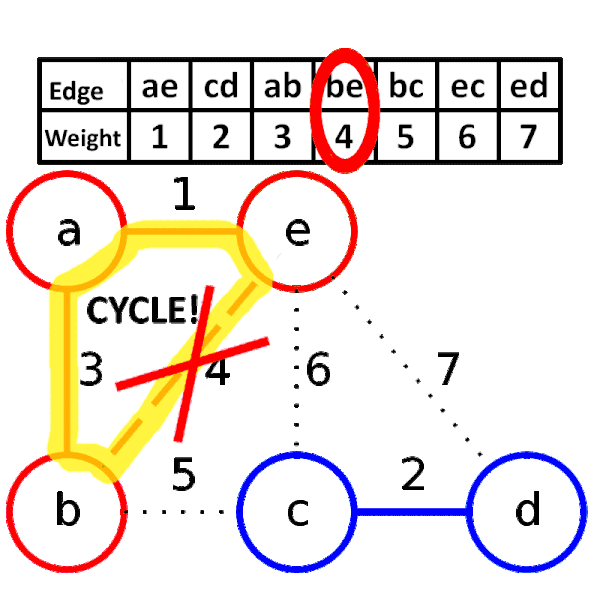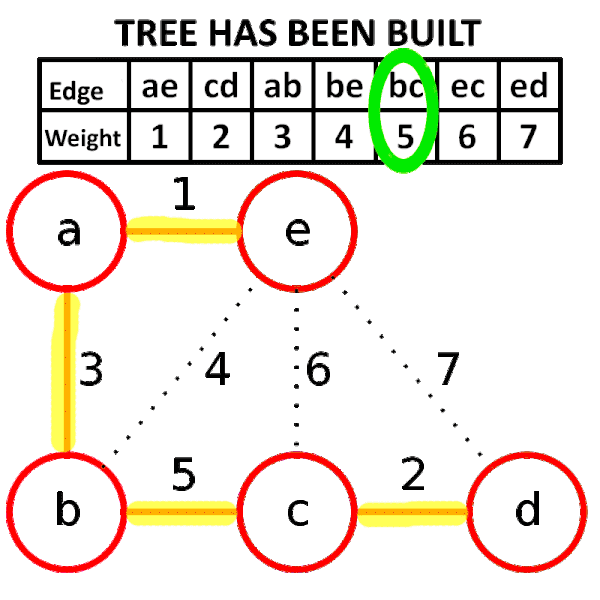
2. 가중치가 가장 낮은 간선부터 하나씩 선택한다. 단, 선택한 간선으로 인해 사이클이 발생한다면 제외한다.
3. $n-1$개의 간선이 선택될 때까지 반복한다.

---

사이클 발생 유무를 감지하기 위해 Union-Find를 사용한다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int parent[10001];

int Find(int x) {
    if (parent[x] == x) return x;
    return parent[x] = Find(parent[x]);
}

void Union(int a, int b) {
    a = Find(a);
    b = Find(b);
    parent[a] = b;
}

int main() {
    vector<vector<int>> edges; // { 가중치, 출발 정점, 도착 정점 }
    
    // 가중치를 기준으로 오름차순 정렬한다.
    sort(edges.begin(), edges.end());

    for (int i = 1; i <= V; i++) {
        parent[i] = i;
    }

    int total = 0;
    int count = 0;

    for (const auto& edge : edges) {
        int cost = edge[0];
        int u = edge[1];
        int v = edge[2];

        // 부모가 다르면 사이클이 발생하지 않는 경우이다.
        if (Find(u) != Find(v)) {
            Union(u, v);
            total += cost;
            count++;
            
            if (count == V - 1) break;
        }
    }

    return 0;
}

---

크루스칼 알고리즘의 시간복잡도는 $O(ElogE)$인데, 이는 간선 정렬에서 비롯된 것이다. 경로 압축을 적용한 Union-Find의 시간복잡도는 상수 시간에 근사하기 때문에, 이를 모든 간선에 대해 적용하는 경우 $O(E)$이기 때문이다. 역시 $E \leq V^2$이므로, $O(ElogV)$라고 표현하기도 한다.