그래프 탐색, BFS와 DFS

📌 BFS란?

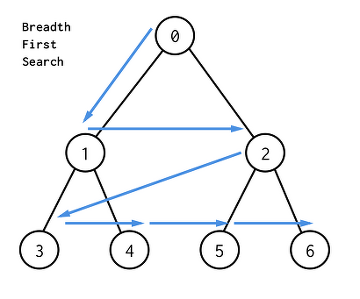
Breath-First Search, BFS 는 그래프를 탐색하는 알고리즘이다. 출발 노드로부터 가까운 노드부터 우선적으로 탐색한다. 이는 레벨 단위로 진행된다.

📌 동작 방식

1. 먼저 시작 노드를 선택하고, 거리를 0으로 설정한다.
2. 거리가 d 인 모든 노드들을 확인하며 해당 노드와 연결된 노드들 중 방문하지 않는 노드들을 방문 처리한다. 이때 방문하는 노드들은 거리가 d+1 이 된다.
3. 이 과정을 더 이상 새로운 노드가 발견되지 않을 때까지 반복한다.

여기서 ‘거리’란 트리의 레벨과 동일한 의미이다.

📌 특징

• 가장 중요한 특징은 가중치가 없는 그래프에서 시작 노드로부터 다른 모든 노드까지의 최단 경로를 보장한다는 것이다. 가까운 노드부터 차례로 방문하기 때문이다.
• 문제에 해가 존재하는 경우 유한한 시간에 그 해를 반드시 찾을 수 있다.
• 보통 FIFO 특징을 가지는 queue 를 통해 구현한다.
• 각 노드의 방문 상태를 확인해야 한다. 이미 방문한 노드를 방문하게 되면 알고리즘 효율이 크게 떨어지며 무한 루프에 빠질 수 있다.

📌 복잡도

노드의 수를 $V$, 간선의 수를 $E$라고 하고, 그래프는 무방향 그래프라고 하자.

시간복잡도

그래프를 어떻게 구현하느냐에 따라 시간복잡도가 달라진다.

인접 리스트로 구현한 경우 노드 u 의 모든 인접 노드를 찾는 데 걸리는 시간은 $O(deg(u))$에 비례한다. 모든 노드의 차수의 합은 $2E$이므로, 간선을 탐색하는 대 걸리는 시간은 $O(E)$이다. 스택에 노드을 삽입/삭제하는 연산은 $O(1)$이므로, 이를 모든 노드에 대해 진행하는 데 걸리는 시간은 $O(V)$이다. 따라서 전체 시간복잡도는 $O(V+E)$이다.

인접 행렬로 구현한 경우 노드 u의 모든 인접 노드를 찾기 위해 $V$개의 노드를 모두 탐색해야 하므로, 걸리는 시간은 $O(V)$이다. 이 작업을 모든 노드에 대해 수행하면 간선 탐색에 걸리는 시간은 $O(V^2)$이다. 따라서 전체 시간복잡도는 $O(V^2)$이다.

공간복잡도

최악의 경우 모든 노드가 큐에 삽입될 수 있으므로 공간복잡도는 $O(V)$이다. 또한 방문 배열의 크기는 노드의 개수에 비례하는 공간을 가져야 하므로 방문 배열의 공간복잡도는 $O(V)$이다. 따라서 전체 공간복잡도는 $O(V)$이다.

📌 구현

알고리즘 문제를 많이 풀어본 것은 아니지만, 경험 상 BFS는 격자 그래프가 주어지는 경우가 많았다. 먼저 격자 그래프에서 BFS를 구현하는 방법을 알아보자.

import sys
from collections import deque

# n: 행, m: 열
n, m = map(int, sys.stdin.readline().split())

# 1: 이동 가능, 0: 벽
graph = []
for _ in range(n):
    graph.append(list(map(int, sys.stdin.readline().strip())))

# (x좌표, y좌표) 튜플 저장
# (0, 0)이 시작 좌표라고 가정한다.
queue = deque([(0, 0)])

# 방문하지 않은 곳은 0으로 초기화
visited = [[0] * m for _ in range(n)]
visited[0][0] = 1

# 방향 벡터
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]

while queue:
    x, y = queue.popleft()

    for i in range(4):
        nx = x + dx[i]
        ny = y + dy[i]

        # 그래프 범위 내에 있는지 확인
        if 0 <= nx < n and 0 <= ny < m:
            if visited[nx][ny] == 0 and graph[nx][ny] == 1:
                visited[nx][ny] = 1
                queue.append((nx, ny))

if visited[n - 1][m - 1] == 0:
    print("방문 불가능")
else:
    print("방문 가능")

격자 그래프 탐색은 보통 동서남북으로 이동하는 경우가 많다. 따라서 현재 다음에 탐색할 좌표를 쉽게 계산하기 위해 dx, dy 같은 방향 벡터를 정의하여 사용하는 것이 편리하다.

만약 최단 거리를 구하고 싶다면 visited[nx][ny] = 1 대신 visited[nx][ny] = visited[x][y] + 1 을 사용하면 된다. 다만 이 경우 초기 방문 배열을 -1 로 초기화하고 시작 좌표에 대한 방문 배열의 값을 0 으로 초기화해야 도착 좌표의 방문 배열 값이 최단 거리가 된다. 아니면 애초에 방문 배열을 0 으로 초기화하고 도착 좌표의 방문 배열의 값에 1을 빼도 된다. 구현하기 나름이다.

import sys
from collections import deque

# n: 정점의 수, m: 간선의 수
n, m, start_node = map(int, sys.stdin.readline().split())

# graph[u][v] = 1: u와 v가 연결되어 있음
graph = [[0] * (n + 1) for _ in range(n + 1)]

for _ in range(m):
    u, v = map(int, sys.stdin.readline().split())
    graph[u][v] = 1
    graph[v][u] = 1

queue = deque([start_node])
visited = [0] * (n + 1)
visited[start_node] = 1

while queue:
    x = queue.popleft()

    for nx in range(1, n + 1):
        if graph[x][nx] == 1 and visited[nx] == 0:
            visited[nx] = 1
            queue.append(nx)
            
if visited[n] == 1:
    print("방문 가능")
else:
    print("방문 불가능")

주어지는 그래프가 인접 행렬이라면 위와 같이 구현하면 된다.

import sys
from collections import deque

n, m, start_node = map(int, sys.stdin.readline().split())

graph = [[] for _ in range(n + 1)]

for _ in range(m):
    u, v = map(int, sys.stdin.readline().split())
    graph[u].append(v)
    graph[v].append(u)

queue = deque([start_node])
visited = [0] * (n + 1)
visited[start_node] = 1

while queue:
    x = queue.popleft()

    for nx in graph[x]:
        if visited[nx] == 0:
            visited[nx] = 1
            queue.append(nx)

if visited[n] == 1:
    print("방문 가능")
else:
    print("방문 불가능")

주어지는 그래프가 인접 리스트라면 위와 같이 구현하면 된다. 사실 그래프 구현 방식만 달라진 것 뿐, BFS의 동작은 동일하다.

📌 DFS란?

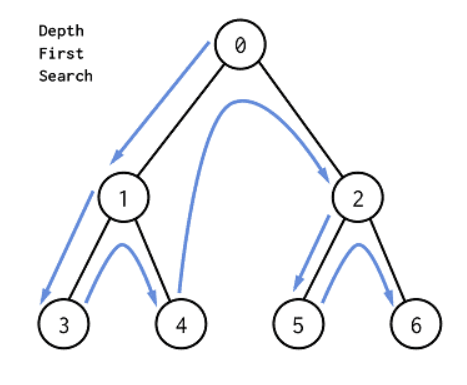
Depth-First Search, DFS 역시 그래프를 탐색하는 알고리즘이다. 출발 노드부터 출발해서 가능한 깊이 탐색하는 방식으로, 더 이상 갈 곳이 없으면 되돌아가서 다른 경로를 탐색한다.

📌 동작 방식

1. 시작 노드를 선택하고 거리를 0으로 설정한다.
2. 거리가 d 인 노드에서 하나의 간선을 선택하여 인접 노드로 이동한다.
3. 이 과정으로 더 이상 새로운 노드를 발견할 수 없을 때까지 반복한다.
4. 더 깊이 내려갈 수 없다면 한 단계 뒤로 되돌아간다. 해당 노드에서 아직 가지 않은 다른 간선이 있다면 해당 간선을 따라 다시 탐색을 진행한다.
5. 최종적으로 시작 노드까지 되돌아왔을 때 더 이상 방문할 새로운 노드가 없다면 탐색을 종료한다.

📌 특징

• DFS는 해를 발견하는 즉시 탐색을 종료하므로 해당 경로가 최단 경로라는 보장은 없다.
• LIFO 특징을 가지는 stack을 사용하거나 재귀를 통해 구현한다.
• 트리의 깊이가 매우 깊어지는 경우 스택 오버플로우가 발생할 수 있다.

📌 복잡도

노드의 수를 $V$, 간선의 수를 $E$라고 하고, 그래프는 무방향 그래프라고 하자.

시간복잡도

BFS와 유사한데, 그래프 구현에 따라 결정되기 때문이다. DFS와 BFS는 탐색 순서만 다르지, 모든 노드를 방문해야 하는 점은 동일하다.

인접 리스트로 구현한 경우 노드 u 의 모든 인접 노드를 찾는 데 걸리는 시간은 $O(deg(u))$에 비례한다. 모든 노드의 차수의 합은 $2E$이므로, 간선을 탐색하는 대 걸리는 시간은 $O(E)$이다. 큐에 노드을 삽입/삭제하는 연산은 $O(1)$이므로, 이를 모든 노드에 대해 진행하는 데 걸리는 시간은 $O(V)$이다. 따라서 전체 시간복잡도는 $O(V+E)$이다.

인접 행렬로 구현한 경우 노드 u의 모든 인접 노드를 찾기 위해 $V$개의 노드를 모두 탐색해야 하므로, 걸리는 시간은 $O(V)$이다. 이 작업을 모든 노드에 대해 수행하면 간선 탐색에 걸리는 시간은 $O(V^2)$이다. 따라서 전체 시간복잡도는 $O(V^2)$이다.

공간복잡도

DFS는 하나의 경로를 가능한 깊이 탐색하므로, 최악의 경우는 가장 깊게 들어가는 경우를 살펴보면 된다. 따라서 그래프의 최대 깊이를 $h$라고 할 때, 스택에 최대 $h$까지의 노드가 들어갈 수 있으며, 따라서 공간복잡도는 $O(h)$이다.

📌 구현

import sys

sys.setrecursionlimit(10**6)

# n: 행, m: 열
n, m = map(int, sys.stdin.readline().split())

# 1: 이동 가능, 0: 벽
graph = []
for _ in range(n):
    graph.append(list(map(int, sys.stdin.readline().strip())))

# 방문하지 않은 곳은 0으로 초기화
visited = [[0] * m for _ in range(n)]

# 방향 벡터
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]

def dfs(x, y):
    visited[x][y] = 1

    for i in range(4):
        nx = x + dx[i]
        ny = y + dy[i]

        # 그래프 범위 내에 있는지 확인
        if 0 <= nx < n and 0 <= ny < m:
            if not visited[nx][ny] and graph[nx][ny] == 1:
                dfs(nx, ny)

if graph[0][0] == 1:
    dfs(0, 0)

if visited[n - 1][m - 1]:
    print("방문 가능")
else:
    print("방문 불가능")

경험 상 보통 스택보단 재귀를 통해 DFS를 구현하는 것 같다.

귀찮으니 격자 그래프에서의 탐색만 살펴보자. 다른 그래프도 BFS와 비슷한 코드로 동작한다.

파이썬으로 구현하는 경우 setrecursionlimit 으로 재귀 깊이 제한을 늘려야 문제를 풀 수 있는 경우가 많다.

📌 BFS vs. DFS

구분	BFS	DFS
구현 방법	queue	stack, 재귀
최단 경로 보장 여부	O	X
탐색 속도가 비교적 더 빠른 상황	목표 노드가 시작 노드에 가까울 때	목표 노드가 깊을 때
시간복잡도	$O(V+E)$ (인접 리스트), $O(V^2)$ (인접 행렬)	$O(V+E)$ (인접 리스트), $O(V^2)$ (인접 행렬)
공간복잡도	$O(V)$	$O(h)$